凸面和均質(zhì)是GOMBOC (字母O上面有來年各個(gè)小點(diǎn)哦)的主要特性。+ p+ b7 g, I. v
不倒翁是非均質(zhì)物體擁有GOMBOC一樣行為的簡(jiǎn)單例子。- @ e) R+ d! D' B% G5 ?
同樣,因?yàn)榘济骟w不能通過表面圓周滾動(dòng),也很容易創(chuàng)造出GOMBOC均質(zhì)凹面體3 ~' q( K8 [( x6 Z: L" d: F
4 A6 n& {. P# K% K+ t

凹面GOMBOC平面圖.
- @- d+ y# X% e5 y1 m3 \) n- W4 _
只擁有唯一一個(gè)穩(wěn)定平衡點(diǎn)的形狀稱作單靜態(tài)體,同時(shí)擁有另外一個(gè)非穩(wěn)定平衡點(diǎn)的稱為單一單靜態(tài)體。
GOMBOC是第一個(gè)凸面均質(zhì)單一單靜態(tài)體。
4 N/ h. N N" ]1 F4 P' @
* e9 [) C/ _6 J5 Q+ W
平面GOMBOC
由于物體重心(G)作用,平面凸形在極坐標(biāo)系中規(guī)定為函數(shù)R(a)。
/ y1 @" F5 k+ l
在水平面上,所有物體都朝著重心降低的方向滾動(dòng)。 R隨著地面降低而變小。 * o/ l1 A' O; Y& D5 j
# S$ F' x; [6 n( Q& q
當(dāng)dR/da = 0時(shí)出現(xiàn)平衡點(diǎn)。R (d2R/da2 > 0)為最小值時(shí),是穩(wěn)定平衡點(diǎn),當(dāng)R((d2R/da2 < 0)為最大值時(shí),是非穩(wěn)定平衡點(diǎn)。R最小值后出現(xiàn)轉(zhuǎn)而最大值,反之亦然。因此,出現(xiàn)穩(wěn)定平衡點(diǎn)和非穩(wěn)定平衡點(diǎn)次數(shù)相當(dāng)。另外,下面原理也可以被證明:
/ D3 b* F/ E% k" H: }
7 B: v. A0 e# n- o6 E
原理 1:
所有平面凸均質(zhì)體至少有2個(gè)穩(wěn)定和2個(gè)非穩(wěn)定平衡點(diǎn)。% i4 {1 f2 f% B7 F4 P8 t5 s: T( l
如果物體只有一個(gè)平衡點(diǎn),相應(yīng)函數(shù)R(a)圖就只能有一個(gè)最大值和最小值。
用直線 R = R0 將物體分成兩部分,函數(shù) R > R0 和 R < R0 具有相等((長度 p)水平投影。 # d9 r- c \2 U. M
相當(dāng)于穿過重心G的直線相應(yīng)把物體切割成薄(R < R0)和厚 (R > R0)兩部分,' ^% _# [/ O1 A% y. \
支撐面沿著直線。
但是達(dá)到平衡的條件是G點(diǎn)不在直線上,應(yīng)該在厚點(diǎn)的這半部分,這與之前所述G點(diǎn)在直線上相矛盾,由此得出原理1正確。
6 W* K( _, ?" k1 h' N1 x) E

編號(hào)為 R(a)的函數(shù)圖(右)以及相對(duì)應(yīng)的物體(左)
正如我們所證明的,不存在平面的GOMBOC型物體。這個(gè)令人驚訝的簡(jiǎn)單事實(shí)是典型數(shù)學(xué)原理的物理模擬:
四頂點(diǎn)定理:: 一條簡(jiǎn)單封閉曲線曲率至少有四個(gè)局部極值
4 X6 j5 }5 V: |
有關(guān)四頂點(diǎn)定理有眾多的概括和相關(guān)幾何定理,有時(shí)這些統(tǒng)稱為四頂點(diǎn)定理。: w1 R1 r2 J& K, A* p6 T
如果不存在三維GOMBOC,這個(gè)事實(shí)將成為四頂點(diǎn)定理家族中的又一新成員。1 K( m7 ^3 }; _3 x9 C6 B
有關(guān)GOMBOC的基本概念
4 N3 V9 O: B- y4 J5 _. ~6 b( G
類似于平面物體,三維體可以定義為重心作用下球坐標(biāo)系中的函數(shù)R(j,q)

三維體在球面坐標(biāo)系中的定義( l' }# c+ D0 w; x$ Z$ y
區(qū)域最小值和最大值R對(duì)應(yīng)穩(wěn)定平衡點(diǎn)和非穩(wěn)定平衡點(diǎn),物體在R的鞍部還有另外一個(gè)平衡點(diǎn)。6 l' N5 i9 A) ]4 B2 O. v& P. K, x1 h. j
根據(jù)龐加萊-霍普夫(Poincaré-Hopf)理論,球體內(nèi)所有同型物體,在這三種情況下,平衡值(由s, u, t,分別代表)都滿足s + u - t = 2。定理1的三種假定情況: . T, O8 ~( P) G$ V d2 ?1 C( \% ]
- a) s > 1,
- b) u > 1,
- c) s + u> 2,
* ~& @9 v! X' @/ `$ l" o
1 L( y+ O% m( q/ a3 F& K( R0 q
a) 和 b)很容易被駁倒
s = t = 1, u = 2時(shí),s > 1為否,
) b5 i+ h: p, {* i

( V" q2 p9 j3 L
- S U2 k% \: @* A& W2 e
: P) q5 d3 l) j# p" Q5 p
i > 1 時(shí) u = t = 1, s = 2
* V! L/ ?, f, ]3 U

- S6 U6 S9 f" q- J5 g4 B6 t
: B) e0 o, F1 q" k# y
( B/ F9 H0 z; |& M0 ~6 R2 C. N
第三種情況可能性存在于Gömböc本身:是否存在三維凸面均質(zhì)s = u =1(t=0)的物體?* f5 Y/ B. d& m: Q3 v6 [
我們可以進(jìn)一步延伸平面理論來證明這種物體存在的不可能性。: o9 M6 b- s9 K0 ~6 `# i
假設(shè)存在這種形狀物體,對(duì)應(yīng)函數(shù)R(j,q)就只能有一個(gè)最小值和一個(gè)最大值。
平面物體用R = R0分割成薄厚相同尺寸的兩部分(以重心點(diǎn)G作為分割,兩部分的空間角度相同)。
如果切割的線條是平面曲線(如:圓),則得出類似二維體的矛盾。 Z# [% t' h9 \. N5 ?9 u3 C
如果是空間曲線,則是類似網(wǎng)球的曲線。
物體分割成上下厚薄兩部分,無法證明G點(diǎn)一定在上半部分。
由此得出平面理論并不適用于三維體。0 U) a, z! L! X5 j* v- K
8 ^' v8 a$ r: F1 z: e& e
" Y0 ^* m) `: O

分割單一單靜態(tài)體厚(黃色)薄(綠色)兩部分的直線是有可能,但并不一定在一個(gè)平面上。
5 Q1 Q: Q3 g' e2 X! ?* ^7 }) `- a( J1 f7 t
論證的失敗為GOMBOC的空間形狀提供了新的想法。% e/ T0 R, S/ @4 G, F5 N& `
運(yùn)用雙參數(shù)閉合公式,可以分析出適當(dāng)參數(shù)值得出s = u = 1物體。" E6 Q4 x. h0 j; A0 l0 K X. g
受凸面體限制,構(gòu)造出的物體近似于球體。6 Z4 h5 r2 r2 B2 N2 {
構(gòu)造出的形狀可以從理論推斷出存在GOMBOC可能性,但是否具有單一單靜態(tài)體(從視覺上可以明顯看出)特性仍然是個(gè)疑問。+ H+ i* b/ Z1 M$ _
1 t" A6 m) z) V
' M+ _" `$ l* J- U$ M( X

應(yīng)用于論證的雙參數(shù)物體圖形
“真正的"GOMBOC: \5 U+ D& Q7 N( |1 S! J
9 l: K3 X3 L3 t4 f
通過理論論證為什么不能找到一個(gè)具有特殊形狀的物體?
是因?yàn)檎撟C公式不好還是因?yàn)槭”澈箅[藏著更深層的原因?
GOMBOC具有類似球體的形狀,但在羅得島上2000多個(gè)卵石中也沒能找到這種形狀,這種形狀如果離球體“很遠(yuǎn)"就不可能是s = i = 1。盡管尋找這種物體很困難,但是通過另一種途徑卻可以構(gòu)造出GOMBOC的形狀。以下的圖示是基于網(wǎng)球的理念。它表面由簡(jiǎn)單圖形組成(圓柱,橢圓形,錐形)和平面。顯而易見,這種形狀屬于凸面體。通過數(shù)值積分算出其重心應(yīng)稍低于原先的位置,通過這些事實(shí),我們可以簡(jiǎn)單判斷出這個(gè)形狀屬于單一單靜態(tài)體。當(dāng)然,無數(shù)的形狀都可以有這些特性,而以下圖形只是其中的一種。構(gòu)造出來的GOMBOC樣品略有不同:它由很多圖塊組成,這使得穩(wěn)定平衡特性更健全,滾動(dòng)物體的力學(xué)表現(xiàn)更加直觀。9 c0 O! }/ z: F1 o* I5 k& U
6 v3 ]# L. A5 o$ n4 I! W X
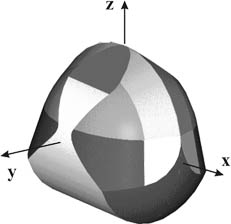
簡(jiǎn)單的圖塊拼接到一起構(gòu)成GOMBOC
$ O d" i6 k' S

在R=穩(wěn)定的情況下,GOMBOC的輪廓線能明顯具有網(wǎng)球形狀
1 |6 v. e0 ?& |; ]: k