橢圓與圓的重合長度如何最優控制？

查看數: 4772 | 評論數: 11 | 收藏 0

關燈 | 提示：支持鍵盤翻頁<-左右->

發布時間: 2019-6-27 14:56

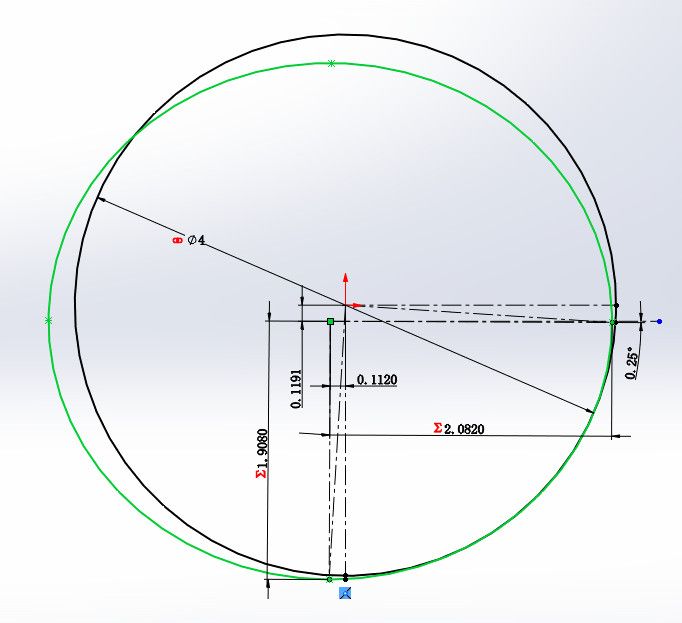
本帖最后由 sxyxs13754 于 2019-6-27 14:58 編輯最近由于設計要求，想求橢圓和圓在第四象限區最大的重合長度，圓中心為原點，x+軸方向水平向右，y+方向垂直向上。目標 ...

回復

小小cb 發表于 2019-6-28 10:25:04

sxyxs13754 發表于 2019-6-27 15:54
你說得對，理論上的重合不可能
重定義一下我們實際加工應用中 "重合" 的意思：

還是從數學角度看，橢圓方程x2/a2+y2/b2=1；當a=b的時候，橢圓就變成圓了；所以你要這個橢圓非常接近圓，但實際又是一個橢圓，那只要a特別接近b，但a又不等于b，就可以實現了；

sxyxs13754 發表于 2019-6-28 08:58:19

魍者歸來發表于 2019-6-27 16:54
從數學的角度講，重合部分的長度是0。

以上是廢話。按樓主后面提到的需求，可以這樣考慮：就以0.001為【 ...

多謝魍者說的思路……最優解只能軟件優化，matlab永遠的傷

sxyxs13754 發表于 2019-6-28 08:33:03

pacelife 發表于 2019-6-27 17:27
有一個問題是這個重合部分會不會是不連續的曲線

不會，我要的曲線是橢圓，圓是我逼近的目標。

遠祥 發表于 2019-6-27 20:25:37

這都是零小數點后好幾位了啊！計算無法很準確的。

17567410 發表于 2019-6-27 17:42:30

本帖最后由 17567410 于 2019-6-27 17:49 編輯

該曲率的最大弧長可以求出來嗎？或者是弧長的最大值。

17567410 發表于 2019-6-27 17:41:43

該曲率的最大弧長可以求出來嗎？

pacelife 發表于 2019-6-27 17:27:24

有一個問題是這個重合部分會不會是不連續的曲線

pacelife 發表于 2019-6-27 17:25:09

樓主不妨先把方程和不等式列出來看看

魍者歸來 發表于 2019-6-27 16:54:44

從數學的角度講，重合部分的長度是0。

以上是廢話。按樓主后面提到的需求，可以這樣考慮：就以0.001為【條件】將圓半徑線與橢圓的交點等于0.001的點求出來，不用考慮橢圓轉角，直接計算這些點之間的距離，如果想不到好方法就用軟件窮舉，選出距離的最大值就ok了

		自動登錄	找回密碼
密碼			注冊會員